岩手県立総合教育センター教育研究(1999)

創造的に考える力を育てる算数・数学科の学習指導に関する研究

−自らの課題を追究する活動をとおして−（第１報）

目　　次

１　研究の目的
２　研究の基本構想図
３　基本的な考え方
　(1) 創造的に考える力の意味
　(2) 創造的に考える力を構成する要素
　(3) 創造的に考える力を育てる意義
　(4) 自らの課題を追究する活動
　(5) 自らの課題を追究する活動の進め方
４　学習指導試案作成のための調査
　(1) 調査の概要
　(2) 調査の内容
　(3) 調査の結果
　(4) 学習指導試案作成上の留意点
５　創造的に考える力を育てる算数・数学科の学習指導試案
６　研究のまとめと今後の課題
　(1) 研究のまとめ
　(2) 今後の課題

＜主な引用・参考文献＞

平成１１年度（第４３回）　岩手県教育研究発表会　算数・数学分科会　研究授業
小学校　第４学年　単元名「直方体と立方体」　学習指導案

１　研究の目的
　自ら学び自ら考える力の育成が求められている今、算数・数学科の学習指導に必要なことは、児童生徒が自分の課題を見つけ、既得の知識や経験をもとにしながら解決法を見いだしたり、それをさらに発展させて考えたりすることができる創造的に考える力を育てることだと考えます。
　しかし、児童生徒の実態には、単純な計算や公式に数値をあてはめて手順通りに答えを求めることは得意でも、学んだことを組み合わせたり見方を変えたりして問題を解くことは苦手な傾向がみられます。これは、授業における自力解決や比較検討の学習が、児童生徒一人一人の真に考え解決する活動になり得ていないことや、身に付けたことをその後の学習や生活に生かす指導が十分になされていないことによるものではないかと思われます。
　そこでこの研究では、単元の学習に児童生徒が自らの課題を追究する活動を位置づけることによって創造的に考える力を育てる学習指導の在り方を明らかにし、算数・数学の学習指導の改善に役立てようと考えました。

２　研究の基本構想図
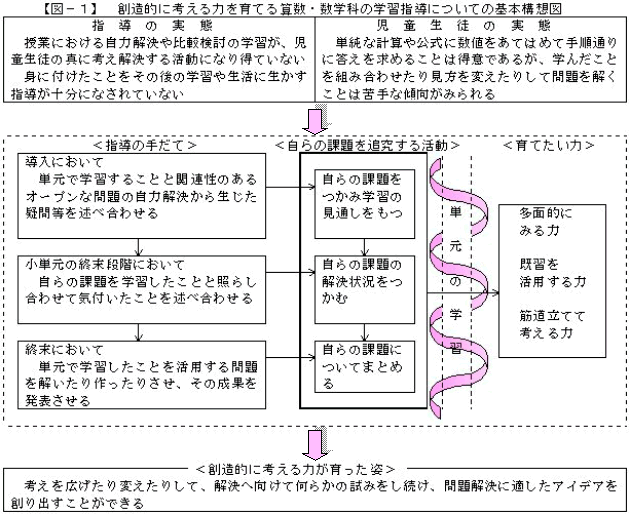
　【図−１】は、この研究の基本構想を図に表したものです。
　図中の ＜指導の手だて＞ ＜自らの課題を追究する活動＞ ＜育てたい力＞ ＜創造的に考える力が育った姿＞ について、その基本的な考え方を以下の項で述べることとします。

３　基本的な考え方

(1) 創造的に考える力の意味
　この研究では、創造的に考える力を「考えを広げたり変えたりして、解決へ向けて何らかの試みをし続け、問題解決に適したアイデアを創り出す力」ととらえました。
　「考えを広げたり変えたり」することについては、創造性についての先行研究で述べられている直観的思考や拡散的思考を重視したいと考えたことによります。児童生徒が、解決の過程におけるひらめきや疑問などをもとにして、様々な角度から解決を試みることができるようにしたいと考えました。その試みを「し続ける」とは、結果が出ればそれで終わりとするのではなく、得た結果に対し「さらに工夫はできないだろうか」「他の方法はないだろうか」と考えたり、新たな課題を見いだし追究したりすることです。また、「アイデア」とは、児童生徒一人一人にとってのアイデアであり、それを「創り出す」ことは、既往の学習や経験により身に付けた複数の事柄を結び付けたり、組み替えたりして順序よく考えを進めることによって可能になると考えました。
　これら、創造的に考える力の本研究におけるとらえは、先行研究をよりどころとして、以下のように考えたことによります。
　「創造性」の定義には、恩田（1994）の「創造性とは、ある目的達成または新しい場面の問題解決に適したアイデアを生み出し、あるいは社会的文化的または個人的に新しい価値あるものをつくり出す能力およびそれを基礎づける人格特性である」というものがあります。この「創造性」は「創造的思考力」「創造的表現力、技能」「創造的態度」の３つの側面に分けてみることができます。
　この定義の中の「新しい」という意味には、社会的文化的に価値ある質的変革をもたらす場合と、個人にとって新しい経験という場合があり、これは、マズローの「創造性には２種類あって、一つは、いわゆる天才といわれる人たちが社会的レベルでの創造・創作を行うような特殊な才能の創造性で、他の一つは誰でもが日常生活の中で発現し得る独創性のような自己実現の創造性である」という考えによるととらえました。教育で課題とされる創造性は後者であり、問題解決をとおして得る成就感などによる自己肯定と、新しい認識や体験による自己否定をくり返しながら自己実現を図ることが、誰にもでき得る創造性です。
　数学教育における創造性については、植村（1999）が、「新しい価値あるものやアイデアを創り出す能力と、それを可能にする数学的な考え方や数学的表現力、創造的思考に対する積極的な態度である」と述べています。
　創造的思考とは、恩田(1974)によると、「新しい場面の問題解決に適したアイデア、あるいは創造活動のイメージをつくり出す思考であり、想像と思考の働きが統合されたものとして見ることができる」ことです。
　「想像と思考の働きが統合されたもの」ととらえることについて、ブルーナーは、創造的思考を直観的思考と分析的思考（論理的思考）の両方の働きが統合されたものとしてとらえ、未知の世界に入るためには分析的思考だけでは十分でなく、直観的思考が必要であることを強調しています。
　また、ギルフォードは、創造的思考を拡散的思考と収束的思考とが統合されたものと見なしています。拡散的思考は、考え方を多方面に広げ多種多様に変えていく思考であり、収束的思考は一定の目的、方向に導かれていく思考のことです。ギルフォードはこの拡散的思考を創造性の特質として重視しました。

(2) 創造的に考える力を構成する要素
　創造的に考える力を構成するおもな要素は、多面的にみる力、既習を活用する力、筋道立てて考える力ととらえました。
　多面的にみる力は、考えを広げたり変えたりする、拡散的な思考に必要な力です。「多面的」には、問題自体を多面的にみることと解決する方法を多面的にみることが考えられます。この力の育成が、多様に発想することのできる児童生徒を育てることに結びつくと考えました。
　既習を活用する力は、考えを広げたり変えたりするときや解決に向けての試みをし続けるときに必要な力です。この力の育成が、これまでに身に付けてきたものをあてはめたり、結び付けたり、組み替えたりすることのできる児童生徒を育てることに結びつくと考えました。
　筋道立てて考える力は、問題解決に適したアイデアを「創り出す」ために必要な力です。この力の育成が、多面的にみて気付いたことや身に付けたものなどの中から解決に必要なものを見いだし、よりよい解決のために順序よく考えを進めることのできる児童生徒を育てることに結びつくと考えました。

(3) 創造的に考える力を育てる意義
　児童生徒が社会の変化に主体的に対応し行動できるようにするために、「自ら学び自ら考える力」を育成することが、今日の教育課題です。これは、いつどのような状況下でも、物事の解決には、自分が身に付けたものをもとにして、自分なりの構想をもち、対処していくことができるような力を育てる、知識の記憶に終始しない教育が必要だととらえることができます。
　算数・数学の指導では、このような力を育てていくために、概念形成、原理把握の学習や問題解決の学習をとおして、既習の事柄を用いて考えたり、多様な考え方や解決の方法を比較検討したりする学習を展開してきています。
　しかし、児童生徒には、計算は得意だが考えることは苦手な傾向や、一つの答えを求めることはできるが多様な見方や考え方が十分ではない傾向が見られることが、国際比較調査などから報告されています。これらの実態を清水（東京学芸大学教育学部）は、「新しい観点から考えようとする着想に乏しい」「異なる考えを受け入れることに抵抗を示す」と指摘し、児童生徒の思考が「硬直している」とも表現しています。
　このような実態の解消には、物事を固定的にみたり考えたりすることなく、多様に発想し、いろいろなことに気付き、考えることができるように多面的にみる力を育てることが必要です。同時に、学習や経験によって身に付けたことを有効に用いることができるように、既習事項を活用する力が必要です。また、物事を正しく解決していくためには、多様な発想や既習事項の中から必要なものを取り出し、順序よく考えを進めることができるように筋道立てて考える力が必要です。
　これらの力の育成は、すなわち「考えを広げたり変えたりして解決へ向けて何らかの試みをし続け、問題解決に適したアイデアを創り出す」創造的に考える力を育てることであり、ひいては「自ら学び自ら考える力」の育成へと結びつくものであると考えます。

(4) 自らの課題を追究する活動
　算数・数学の授業では多くの場合、指導のねらいに即した問題が提示され、問題構造をとらえて、新たに解き明かさなければならないことが「学習課題」として、かかげられます。
　はじめに問題が提示されたとき、それを読んで児童生徒は、それぞれ、個々様々にふと何かを思い浮かべたり、考えたりしていることと思います。そのような、自分の内側からわき出た思いや疑問にこだわって学習を進めさせたいと考えました。なぜならば、自分自身の思いや疑問の解決が、児童生徒の主体的な学びへつながると考えるからです。本研究では、そのような児童生徒一人一人の素朴な疑問や思い、こだわりなどを「自らの課題」とします。
　自らの課題を追究する活動とは、児童生徒が、自らの課題の解決に向けて自分の考えをもち、それについて述べ合うことをとおしてよりよく解決し、さらなる課題をもって考える活動です。
　物事の解決のためには、既往の学習や体験と照らし合わせて、多様な方法で試してみることが必要ですが、それが、一人でなされていては限度があります。このとき大切なのは、他の意見に耳を傾け、それをもとによりよく解決していくことです。したがって、自らの課題を追究する活動においては、児童生徒が互いに考えを述べ合うことを重視します。この活動によって、一人では気付くことのできなかった幾通りかの解決の仕方に気付いたり別の考えがひらめいたり、また、新たな課題が生じたり課題の修正が必要になったりすることと思います。児童生徒が互いの考えを述べ合うことにより、視野を広め自分の考えをより客観的にとらえ、正しく解決することができると考えました。

(5) 自らの課題を追究する活動の進め方
　次頁【表−１】は、「自らの課題を追究する活動の進め方」を示したものです。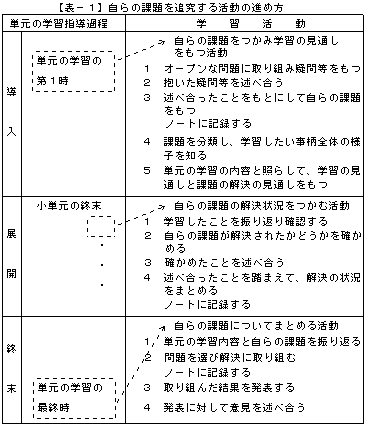
　自らの課題を追究する活動は、単元の学習と並行して行い、単元の学習指導過程に「自らの課題をつかみ学習の見通しをもつ活動」「自らの課題の解決状況をつかむ活動」「自らの課題についてまとめる活動」を位置付けます。
　それぞれの活動は以下のように行います。
　「自らの課題をつかみ学習の見通しをもつ活動」は、単元の学習における導入段階に位置付けます。この活動では、始めに単元の学習内容を含むオープンな問題を提示します。ここでは、問題の解決が目的ではなく、気付いたことや疑問をもとに自らの課題をつかむことがねらいです。そこで、初めに抱いた各自の素朴な疑問等を、互いに述べ合う活動をとおして、よりよい自らの課題としていきたいと思います。その後、各自の課題を分類することにより、学習したい事柄全体の様子を知り、単元の学習の内容と照らして、学習の見通しと課題の解決の見通しをもつようにしていきます。
　「自らの課題の解決状況をつかむ活動」は、単元の学習の展開段階において、小単元などのようにひとまとまりの学習が終わったところに位置付けます。ここでは、自らの課題が解決されたかどうかを確かめる活動を行います。自分で確認した後は、児童生徒相互に結果について意見を述べ合うようにします。他の意見を聞くことにより、一人では見いだせないことを得たり、新たな課題を発見したりし、次の学習へと結び付けるようにしたいと考えたからです。
　これらの活動で、児童生徒が設定した自らの課題やその解決の状況については、各自ノートなどに記録させておくようにします。
　「自らの課題についてまとめる活動」は、単元の学習における終末段階に位置付けます。
　ここでは、学習のまとめとして問題解決に取り組みその結果を発表し合う活動を行います。
　取り組む問題は、生活への活用が意識できるような内容とし、複数の中から児童生徒に取り組みたいものを選択させます。また、児童生徒が自分で問題を作って取り組むことも認めるようにします。
　活動の始めに、単元の学習内容と自らの課題を、ノートの記述をもとに振り返らせ、その後、問題を選択させて、これまでの学習と結び付けながら解決に取り組むようにさせたいと考えました。
　発表は、問題の解決にあたって既習のどのようなことを用いたかを説明したり、これまでの自らの課題と結び付けて話したりさせたいと思います。ここでも、発表に対して意見を述べ合い、さらなる課題の発見へと進めるようにしていきます。

４　学習指導試案作成のための調査
　創造的に考える力を育てる算数・数学科の学習指導試案を作成するにあたり、「創造的に考える力を育てる算数・数学科の学習指導についての基本的な考え方」に基づいて、実態調査を行いました。

(1) 調査の概要
　【表−２】は、実態調査の概要を示したものです。

(2) 調査の内容
　創造的に考える力を育てるための手だてである「自らの課題を追究する活動」を取り入れた学習を進めるにあたり、以下の７点について実態を把握したいと考えました。

1	算数・数学の学習に対するイメージや学習時の困難点
2	算数・数学の学習態度の積極性
3	「考えること」についての意識
4	単元の学習の導入でオープンな問題を用いた学習を行うが、これを生徒達は抵抗なく受け止めることができるかどうか
5	算数・数学の問題に取り組む意欲
6	児童生徒が安心して、有効に活動できる学習形態
7	述べ合う活動を行う際の留意点

　これらを踏まえて、実態調査問題を作成しました。【表−３】は、その項目と内容を示したものです。

(3) 調査の結果
　調査は13の設問で実施しましたが、本稿では、そのうちの６つの設問について、結果を示し考察を行います。

ア　わからないことがあったときの行動　（設問６） 　【図−２】は、算数・数学の勉強をしていてわからないことがあったときにどうするのかを調べた結果です。 　どの学年においても、わからないときは「誰かに聞く」が、最も多く、50％ 以上を占めていることがわかります。 　小５から上の学年で次に多いのは、「誰にも聞かな いで教科書や参考書などで、自分で調べる」であり、学年が上がるにつれてその割合は増えています。児童生徒は、わからないことがあったとき、そのままにせず、なんとかしようとしていることがわかります。

イ　問題をはやく解き終わったときの行動　（設問５） 　【図−３】は、算数・ 数学の授業中に友達よりも問題をはやく解き終わったとしたらどうしたいかを調べた結果です。 　　　　　　　　　　　　　　　　　　　注：【図−２】に同じである 　学年別に多い項目をみると、小４は、「みんなが終わるまで静かに待っていたい」「合っているかどうかを自分で確かめたり、ほかの解き方を考えたりしたい」「次に何をするか先生に聞いて、言われたことをしたい」が、26％〜28％です。小５は、「みんなが終わるまで静かに待っていたい」「合っているかどうかを自分で確かめたり、ほかの解き方を考えたりしたい」「友達と答えが合っているかどうか話し合いたい」が、23％〜26％です。小６は、「次に何をするか先生に聞いて、言われたことをしたい」「友達と答えが合っているかどうか話し合いたい」が29％です。中１は、「友達と答えが合っているかどうか話し合いたい」が最も多く58％、次いで「合っているかどうかを自分で確かめたり、ほかの解き方を考えたりしたい」の23％です。中２は、中１と同様に「友達と答えが合っているかどうか話し合いたい」が最も多く42％、 次が、「みんなが終わるまで静かに待っていたい」の21％です。高２は、「合っているかどうかを自分で確かめたり、ほかの解き方を考えたりしたい」が34％、「友達と答えが合っているかどうか話し合いたい」が32％です。 　どの学年でも、「合っているかどうかを自分で確かめたり、ほかの解き方を考えたりしたい」「友達と答えが合っているかどうかを話し合いたい」が上位に選択されていて、特に中・高生では、後者の占める割合が高いことがわかります。「先生に言われたことをしたい」は、小学生にみられますが、中・高生ではほとんどありません。また、「静かに待っていたい」は、小４で28％と最も多く、他の学年は10〜20％台です。児童生徒の行動の傾向は学年によって様々ですが、時間を有効に使って、学習に前向きに取り組もうとしていることがわかります。

ウ　考えることについてのイメージ　（設問10)
　次頁【図−４】は、算数・数学の勉強での「考える」という活動に対する児童生徒の意欲やイメージを８観点で調査した結果です。「かなりそう思う」「ややそう思う」というプラス傾向の解答をまとめてグラフに表しました。
　設問10−６，10−７より、80％以上の児童生徒が、「考えることは、大切だ、必要だ」ととらえていることがわかります。
　設問10−８より、「考えることを進んでしたい」と思うのは、小４の80％が最も多く、学年が進むにしたがって減る傾向であることがわかります。類似の傾向は、設問10−５にもみられます。「考えることはすき」と思うのは、小４の60％が最も多く、学年が進むにしたがって減る傾向がみられます。
　設問10−２，10−４より、「考えることはやさしい、簡単」と思うのは、小学生に40％〜60％みられます。中・高生でそう思っているものは、20％前後です。
　設問10−３より、「考えることは夢中になる」と思っている児童生徒は50％以上で、設問10−１からは、「考えることはおもしろい」と思っている児童生徒が40％以上であることがわかります。いずれも学年が進むにしたがって減る傾向ですが、高２で増えています。
　以上のことをまとめると、児童生徒の約80％は考えることは必要で大切だと思っていて、約50％は、考えることがおもしろく、夢中になることであり、好きだと思っているといえます。しかし、学年が進むにつれて、考えることはむずかしくなると感じていることがわかります。
　児童生徒には、一人一人が真に考え、知的おもしろさを味わうことのできる学習活動が必要だと思われます。

エ　答えが一つの問題とオープンエンドの問題のどちらを選ぶか　（設問11） 　【図−５】は、答えが一つの問題とオープンエンドの問題のうち、どちらか一つを選んで取り組むとしたらどちらを選ぶかを調べた結果です。中１を除いた５つの学年で、答えが一つの問題を選んだ児童生徒が、半数を超えていることがわかります。 　【表−４】は、それぞれの問題を選んだ理由をまとめたものです。 　答えが一つの問題を選んだ理由は、どの学年でも「簡単そうだから」が多く、容易に取り組むことができ、難なく解決できることを一番にとらえて選んだことがわかります。 　また、オープンエンドの問題を選んだ理由は、解き方や答えがいろいろ出せるおもしろさや自分の考えを自由に進めることができるよさを感じて選んだことがわかります。 　なお、児童生徒の問題の選び方と算数・数学の成績に関連があるかどうかを調べてみましたが、明記できる傾向はみられませんでした。

オ　問題解決への関心・意欲　（設問12） 　【図−６】は、カレンダーにならぶ数の規則性を知り、その後どうしたいかを調査した結果です。 　５選択肢のうち最も多い項目は、小４、小５で、「なぜそうなるのか理由を知りたい」で、約45％です。小６と中１で最も多いのは、「なぜそうなるのか理由を知りたい」「本当かなと思い別のところも調べてみる」で、中２、高２では、「本当かなと思い別のところも調べてみる」でした。「ほかのきまりをみつけたい」と答えたものが、小４、小５に約20％、小６、中１に約30％みられました。 　このことから児童生徒には、示された事柄に対して調べてみようとする積極性があるといえます。

カ　自分にあっている勉強の仕方　（設問７） 　【図−７】は、算数・数学の授業で自分にあっていると思う学習の仕方を調べた結果です。 　小４から中１で最も多いのは、「先生や学級のみんなと一緒に話し合いながら勉強を進めていく」仕方で、中２、高２では、「先生がみんなに説明してくれるのを聞いて勉強していく」仕方でした。この項目は、小６、中１が２番目に多く回答しているものです。高２で２番目に多いのは、「一人一人で勉強を進めて、わからなくなったら先生に教えてもらう」という勉強の仕方です。 　学年に応じて、様々な学習の形態を工夫し、自力でじっくり解いたり、複数でそれぞれの考えについて話し合い、考えを深めたりする学習が大切と思われます。

(4) 学習指導試案作成上の留意点
　実態調査の結果から、学習指導試案作成上の留意点を次のようにまとめました。

ア	算数・数学の勉強が「いやだ」「できない」「わからない」といったマイナスイメージを抱く状況をつくらない配慮が必要である。興味がわく問題や課題の設定、児童生徒の意見や考えが生かされる学習活動、素朴な疑問が解消される学習活動など、教材、学習形態などに工夫が必要である。
イ	オープンな問題の提示による指導を行う場合には、答えが一つに限らないという見通しをもたせるなど、児童生徒がとまどうことなく学習に取り組むことができるようにし、解き方や答えがいろいろ出せるおもしろさや自分の考えを自由に進めることができるよさを感じることができるようにする。
ウ	考えを述べ合う活動では、自分の考えを気軽に話せるような形態の工夫が必要である。二人組での学習、少人数グループでの学習など考えを述べ合う活動の人数を変えたり、二人組やグループの編成の仕方に工夫が必要である。
エ	児童生徒の発表や述べ合う活動では、他が気付いたことをもとに自分の課題を解決したり、新たな課題に気付いたりできるようにし、それらのことをとおして、互いのよいところを自分の学習に生かすことを学ばせたい。
オ	学習を振り返るときに、自分の学習の過程がわかるような記録の仕方について指導が必要である。

５　創造的に考える力を育てる算数・数学科の学習指導試案

　創造的に考える力を育てるための自らの課題を追究する活動は、前述185頁の【表−１】に示したように進めます。この進め方のうち、�@学習の導入で提示する問題、�A学習の終末で提示する問題、�B述べ合う活動の仕方、�C自らの課題を解決する活動の記録の仕方、�D発表の仕方について、以下のように考えました。

�@　学習の導入で提示する問題
　学習の導入で提示する問題は、単元で学習する内容を含んだオープンな問題を検討し設定する。形式は、文章によるもののほか、情景図、統計資料などの表やグラフなどが考えられる。問題の内容は、条件過剰または不足のものとしたり、文末表現は「〜を求めましょう」ではなく「〜を調べましょう」とするなど、児童生徒によっていろいろに考え課題が設定できるように工夫した問題とする。

�A　学習の終末で提示する問題
　学習の終末で提示する問題は、学習したことを使って解決できる問題を複数用意する。教科書のまとめの問題を活用するほか、オープンな問題も設定する。

�B　述べ合う活動の仕方
　述べ合う活動では、自分の考えを気軽に話すことができるようにしたい。そこで、活動形態を児童生徒の実態に応じて、二人組やグループなど工夫する。二人組は隣同士のほか、ある一定時間内に相手を変える方法もとる。グループによる場合は、グループ編成に工夫が必要である。考えが似ている者同士や全く違う者同士など意図的に編成したり、制限を加えないようにしたりすることが考えられる。
　一つの述べ合う活動が、一つの形態で行われるばかりでなく、二人組からグループへと述べ合う人数を拡大させていくような工夫も必要と考える。

�C　自らの課題を解決する活動の記録の仕方
　自らの課題を解決する活動の記録は、算数・数学の授業で使っているノートを利用する。導入と終末段階の学習ではノート全面を使うが、展開段階の学習では、この活動を記録する特定の場所を例えば、ノートの下段５行とするなどのように決める。記録する内容は、導入と終末段階では、問題への取り組みが中心となり、展開段階では、自らの課題とそれが解決できたかどうかや解決できたと考えたわけなどとする。

�D　発表の仕方
　終末段階で取り組む発表は、主にポスターセッション的な形態とする。授業時間を前後半に分け、前半に発表する者は後半は聴く側となる。発表者は、自分の取り組みについて時間内に複数回説明を行い、より多くの友達に聴いてもらうようにする。聴く側は、一人の発表だけでなく複数の発表を聴き、質問したり意見を述べたりする。

　以上のことを踏まえて、創造的に考える力を育てるための「自らの課題を追究する活動の指導過程試案」を作成しました。
　【表−５】は、自らの課題を追究する活動の指導過程試案です。

６　研究のまとめと今後の課題

(1) 研究のまとめ
　この研究は、単元の学習に児童生徒が自らの課題を追究する活動を位置付けることによって創造的に考える力を育てる算数・数学科の学習指導の在り方を明らかにし、学習指導の改善に役立てようとするものです。
　本年度の研究内容は、創造的に考える力を育てる学習指導についての基本的な考え方を検討し、基本構想を立案し、さらに実態調査によって、児童生徒が抱く算数・数学のイメージや「考えること」についての関心・意欲、学習時の困難点などを把握し、その結果をもとに創造的に考える力を育てる学習指導試案を作成することでした。
　ここでは、それらの研究内容について概括的にまとめます。

�@　創造的に考える力を育てる算数・数学科の学習指導についての基本的な考え方
　先行研究をもとにして「創造性」「創造的思考」についてとらえ、本研究における「創造的に考える力」を「考えを広げたり変えたりして、解決へ向けて何らかの試みをし続け、問題解決に適したアイデアを創り出す力」と定義するとともに、創造的に考える力を育てる学習指導の意義について明らかにすることができた。

�A　創造的に考える力を育てる算数・数学科の学習指導についての基本構想
　創造的に考える力を育てるための手だてである「自らの課題を追究する活動」は、�@単元の学習の導入時にオープンな問題への取り組みから自らの課題と見通しをもつ活動、�A展開時に課題を学習したことと照らし合わせて解決状況をつかむ活動、�B終末時に学習成果をまとめる活動からなる。その活動の意義と進め方について構想することができた。

�B　創造的に考える力を育てる算数・数学科の学習指導試案の作成
　基本構想に基づき、さらに、小学校４，５，６年、中学校１，２年、高等学校２年の児童生徒を対象とした実態調査の結果から明らかになった留意事項を加味して、創造的に考える力を育てる算数・数学科の学習指導試案を作成することができた。

(2) 今後の課題
　来年度は、実践をとおして創造的に考える力を育てる学習指導試案の妥当性及び研究仮説の有効性を検証します。したがって、今後の主たる課題は、創造的に考える力を評価する問題の作成です。先行研究に学び、認知面と情意面から創造的に考える力の変容状況をとらえることができる評価問題を作成したいと考えています。

＜主な引用・参考文献＞

植村哲朗「数学教育における創造性研究の課題」全国数学教育学会誌　数学教育学研究　第５巻 1999
恩田　彰「創造性教育の展開」恒星社厚生閣 1994
横山昌也「数学教育における創造的思考の評価方法に関する研究」数学教育学研究紀要（西日本数学教育学会） 第19号1993
国立教育研究所「小・中学生の算数・数学、理科の成績」東洋館出版社 1998
中島、清水、瀬沼、長崎「算数の基礎学力をどうとらえるか」東洋館出版社 1995

　なお本稿は、平成１１年度岩手県教育研究発表会発表資料「創造的に考える力を育てる算数・数学科の学習指導に関する研究　−自らの課題を追究する活動をとおして−」を再構成したものです。