岩手県立総合教育センター教育研究(2000)
創造的に考える力を育てる算数・数学科の学習指導に関する研究
− 自らの課題を追究する活動をとおして −(第2報)
《 目 次 》
はじめに
1 創造的に考える力の意味
2 創造的に考える力を育てることの意義
3 創造的に考える力を構成する要素
4 自らの課題を追究する活動
5 自らの課題を追究する活動の進め方
6 授業実践
7 創造的に考える力の評価
8 検証計画
9 創造的に考える力の育成状況
おわりに
【引用文献・主な参考文献】
はじめに
この研究は、次のような仮説を設定し、2年間取り組んだものです。
| 研究仮説 算数・数学科の単元の学習過程に、以下の活動を位置付けて指導を行うならば、創造的に考える力を育てることができるであろう。
|
昨年度は、先行研究をもとに、創造性や創造的思考について明らかにしました。また、創造的に考える力の意味やこの力を育てることの意義を明らかにし、研究の基本構想を立案しました。
さらに、実態調査を行い、創造的に考える力を育てる算数・数学科の学習指導試案を作成しました。
本年度は、学習指導試案に基づき「自らの課題を追求する活動」を手だてとした授業実践を試みました。実践の前後には、「創造的に考える力」の評価問題によるテストを実施し、その結果の分析と考察をとおして、学習指導試案の妥当性を検討し、仮説を検証しました。
本稿では、小学校第5学年と中学校第2学年を対象に行った授業実践とその結果を中心にしながら、研究の概要を述べることとします。
1 創造的に考える力の意味
この研究では、創造的に考える力を「考えを広げたり変えたりして、解決へ向けて何らかの試みをし続け、問題解決に適したアイデアを創り出す力」ととらえました。
「考えを広げたり変えたり」することについては、創造性についての先行研究(恩田1994)で述べられている直観的思考や拡散的思考を重視したいと考えたことによります。児童生徒が、解決の過程におけるひらめきや疑問などをもとにして、様々な角度から解決を試みることができるようにしたいと考えました。その試みを「し続ける」とは、結果が出ればそれで終わりとするのではなく、得た結果に対し「さらに工夫はできないだろうか」「他の方法はないだろうか」と考えたり、新たな課題を見いだし追究したりすることです。また、「アイデア」とは、児童生徒一人一人にとってのアイデアであり、それを「創り出す」ことは、既往の学習や経験により身に付けた複数の事柄を結び付けたり、組み替えたりして順序よく考えを進めることによって可能になると考えました。
2 創造的に考える力を育てることの意義
児童生徒が社会の変化に主体的に対応し行動できるようにするために、「自ら学び自ら考える力」を育成することが、今日の教育課題です。これは、いつどのような状況下でも、物事の解決には、自分が身に付けたものをもとにして、自分なりの構想をもち、対処していくことができるような力を育てる、知識の記憶に終始しない教育が必要だととらえることができます。
算数・数学の指導では、このような力を育てていくために、概念形成、原理把握の学習や問題解決の学習をとおして、既習の事柄を用いて考えたり、多様な考え方や解決の方法を比較検討したりする学習を展開してきています。
しかし、我が国の多くの児童生徒には、計算は得意だが考えることは苦手な傾向や、一つの答えを求めることはできるが多様な見方や考え方が十分ではない傾向が見られることが、国際比較調査などで報告されています。これらの実態を清水(東京学芸大学教育学部 1999)は、「新しい観点から考えようとする着想に乏しい」「異なる考えを受け入れることに抵抗を示す」と指摘し、児童生徒の思考が「硬直している」とも表現しています。
このような実態の解消には、物事を固定的にみたり考えたりすることなく多様に発想し、いろいろなことに気付き考えることや、学習や経験によって身に付けたことを有効に用いること、物事を正しく解決していくために、多様な発想や既習事項の中から必要なものを取り出し、順序よく考えを進めることができるようにする必要があると考えました。
このことがすなわち、創造的に考える力の育成であり、ひいては、自ら学び自ら考える力の育成へと結びつくものであると考えました。
3 創造的に考える力を構成する要素
本研究では、創造的に考える力を構成する主な要素を多面的にみる力、既習を活用する力、筋道立てて考える力ととらえました。
多面的にみる力は、考えを広げたり変えたりする、拡散的な思考に必要な力です。「多面的」には、問題自体を多面的にみることと解決する方法を多面的にみることが考えられます。この力の育成が、多様に発想することのできる児童生徒を育てることに結びつくと考えました。
既習を活用する力は、考えを広げたり変えたりするときや解決に向けての試みをし続けるときに必要な力です。この力の育成が、これまでに身に付けてきたものをあてはめたり、結び付けたり、組み替えたりすることのできる児童生徒を育てることに結びつくと考えました。
筋道立てて考える力は、問題解決に適したアイデアを「創り出す」ために必要な力です。この力の育成が、多面的にみて気付いたことや身に付けたものなどの中から解決に必要なものを見いだし、よりよい解決のために順序よく考えを進めることのできる児童生徒を育てることに結びつくと考えました。
4 自らの課題を追究する活動
創造的に考える力を育成するために、算数・数学の学習指導に「自らの課題を追究する活動」を行おうと考えました。
自らの課題とは、児童生徒一人一人の素朴な疑問や思い、こだわりなどです。自らの課題を追究する活動とは、児童生徒が、自らの課題の解決に向けて自分の考えをもち、それについて述べ合うことをとおしてよりよく解決し、さらなる課題をもって考える活動です。
この活動において、創造的に考える力を構成する3つの要素のうち「多面的にみる力」は、主に、児童が互いに考えを述べ合うことをとおして育てたいと考えました。また、「既習を活用する力」は、既往の学習や体験を基に課題を見出したり解決したりすることをとおして育てたいと考えました。「筋道立てて考える力」は、考えを述べ合い学んだ結果をもとに、解決のよりよい方法を選び、それを用いて解くことをとおして育てたいと考えました。
5 自らの課題を追究する活動の進め方
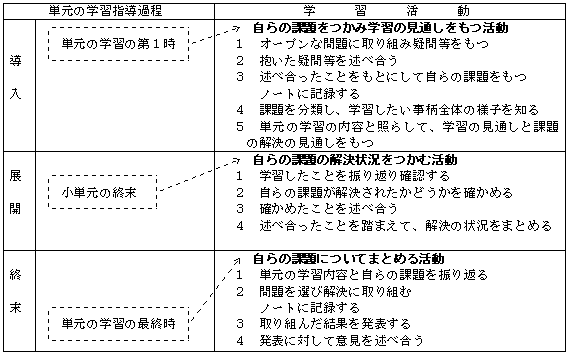
自らの課題を追究する活動は、単元の学習と並行して行い、単元の学習指導過程に「自らの課題をつかみ学習の見通しをもつ活動」「自らの課題の解決状況をつかむ活動」「自らの課題についてまとめる活動」を位置付けます。
「自らの課題をつかみ学習の見通しをもつ活動」は、単元の学習における導入段階に位置付けます。この活動では、始めに単元の学習内容を含むオープンな問題を提示します。ここでは、問題の解決が目的ではなく、気付いたことや疑問をもとに自らの課題をつかむことがねらいです。そこで、初めに抱いた各自の素朴な疑問等を、互いに述べ合う活動をとおして、よりよい自らの課題としていきたいと思います。その後、各自の課題を分類することにより、学習したい事柄全体の様子を知り、単元の学習の内容と照らして、学習の見通しと課題の解決の見通しをもつようにしていきます。
「自らの課題の解決状況をつかむ活動」は、単元の学習の展開段階において、小単元などのようにひとまとまりの学習が終わったところに位置付けます。ここでは、自らの課題が解決されたかどうかを確かめる活動を行います。自分で確認した後は、児童生徒相互に結果について意見を述べ合うようにします。他の意見を聞くことにより、一人では見いだせないことを得たり、新たな課題を発見したりし、次の学習へと結び付けるようにしたいと考えたからです。これらの活動で、児童生徒が設定した自らの課題やその解決の状況については、各自ノートなどに記録させておくようにします。
「自らの課題についてまとめる活動」は、単元の学習における終末段階に位置付けます。ここでは、学習のまとめとして問題解決に取り組みその結果を発表し合う活動を行います。取り組む問題は、生活への活用が意識できるような内容とし、複数の中から児童生徒に取り組みたいものを選択させます。また、児童生徒が自分で問題を作って取り組むことも認めるようにします。
活動の始めに、単元の学習内容と自らの課題を、ノートの記述をもとに振り返らせ、その後、問題を選択させて、これまでの学習と結び付けながら解決に取り組むようにさせたいと考えました。
発表は、問題の解決にあたって既習のどのようなことを用いたかを説明したり、これまでの自らの課題と結び付けて話したりさせたいと思います。ここでも、発表に対して意見を述べ合い、さらなる
課題の発見へと進めるようにしていきます。
6 授業実践
(1) 小学校第5学年の授業実践(小学校 算数 「単位量あたりの大きさ」の学習指導案にリンクされています)
ア 授業計画
授業実践は、平成12年9月6日(水)〜10月5日(木)の期間に、研究協力校の第5学年児童34人を対象に、単元「単位量あたりの大きさ」(東京書籍 新しい算数5)において行いました。
自らの課題を追究する活動を取り入れた単元の学習指導は16時間とし、研究の手だてにかかわる指導は、第1、5、14、15、16時に行うこととしました。それぞれの活動の時間配分は、次のとおりです。
自らの課題をもち学習の見通しをもつ活動は、小単元「平均」と、小単元「単位量あたりの大きさ」「速さ」導入にあたる第1時と第5時に行います。
自らの課題の解決状況をつかむ活動における述べ合う活動の形態は、はじめは隣同士の2人、その後席を離れて自由に紹介し合い意見や感想を話すようにさせようと考えました。これは、算数の学習を苦手と感じていて自分の考えを大勢の前で話す自信がない児童がみられることから、その負担を軽減したいと考えたためです。単元の学習の最後に行う発表は、学級の児童を半数ずつに分けて2グループを作り、授業の前半は1つのグループが発表し後半は残りのグループが発表する形態にしようと考えました。これは、児童がポスターセッション的な発表になれていないことと、指導者が児童全員の取り組みの様子を把握できるようにしたいと考えたためです。
自らの課題を追究する活動を取り入れた学習指導計画は以下のとおりです。
イ 児童の取り組み
自らの課題を追究する活動で児童が抱いた課題とその解決状況の記述のいくつかを以下に示します。
(ア) 小単元「平均」の学習において
(イ) 小単元「単位量あたりの大きさ」「速さ」において
(2) 中学校第2学年の授業実践
ア 単元名 平行と合同 小単元 平行線と角 東京書籍 新編 新しい数学2
イ 展開の概要(8時間扱い)
ウ 授業の概要
(ア) 自らの課題をつかみ学習の見通しをもつ活動(1/8時)
(イ) 学習のまとめ(自らの課題についてまとめる活動)(8/8時)
エ 生徒が設定した主な課題とその解決例
生徒が、自分の課題をもつ活動で設定した主な課題と、まとめで行ったその解決例を示します。
7 創造的に考える力の評価
創造的に考える力の育成状況は、構成要素である「多面的にみる力」「既習を活用する力」「筋道立てて考える力」の変容によりとらえることとしました。
これら3つの力は、児童生徒の行動としてとらえると次のようになります。「多面的にみる」とは「多様に発想することができる」ことであり、「既習を活用する」とは、「身に付けてきたものをあてはめたり、結び付けたり、組み替えたりすることができる」こと、また、「筋道立てて考える」とは、「よりよい解決のために順序よく考えを進めることができる」ことです。創造的に考える力を評価するテスト問題は、このような児童生徒の行動を測定できるように、先行研究等を参考にして作成しました。
また、多面的にみる力の評価規準については、横山(1993)の「数学教育における創造的思考の評価方法に関する研究」における創造的思考を評価する5つの観点を拠り所としました。
これらの観点は、ある問題に対して解決法をたくさん発想できるかどうかといった創造性の量的側面と、他が考えない独自性がみられるかどうかといった質的側面をとらえる観点で、積極性、流暢性、柔軟性、独創性、生産性です。
| ・ | 積極性は、反応したすべての個数に着目する評価観点であり、間違いや重複も数える。 |
| ・ | 流暢性は、反応総数のうちで、正しい反応の個数に着目する評価観点であり、同質であるかどうかは問わない。 |
| ・ | 柔軟性は、正しい反応のうちで、質の異なる反応の個数に着目する評価観点である。数学的にみて異なるアイデアが用いられているかどうかを調べる。 |
| ・ | 独創性は、正しい反応のうちで、頻度の少ない反応の個数に着目する評価観点である。他の児童生徒があまり考えていないような反応をどのくらい出しているかを調べる。 |
| ・ | 生産性は、正しい反応のうち、数学的な価値や実用性を備えているものには、より高い価値があるとみなして付加価値を与える。 |
以下に事前テスト問題の一部を示します。
(1) 多面的にみる力 のテスト問題(小学校5年生・中学校2年生共通)
(2) 既習を活用する力 のテスト問題(小学校5年生)
(3) 筋道立てて考える力 のテスト問題(中学校2年生)
8 検証計画
仮説の検証は、【表1】に示す検証計画によって行うこととしました。
本稿では、主題にかかわるテスト・調査のうち、創造的に考える力の育成状況について、その結果を以下の項で述べます。
9 創造的に考える力の育成状況
(1) 小学校第5学年
ア 創造的に考える力の育成状況
指導試案に基づく授業実践では、創造的に考える力が育っているととらえることのできる記述や取り組みの様子がみられました。この項では、それらが有意差のあるものかどうかをとらえるために、実践の前後に実施した創造的に考える力のテスト結果について分析し考察します。テストは、構成要素である「多面的にみる力」「既習を活用する力」「筋道立てて考える力」について、事前事後に同質の問題を用いて実施しました。
(ア) 多面的にみる力
【表2】は、多面的にみる力の育成状況について、事前・事後テストの結果をまとめたものです。
多面的にみる力は、サイン検定の結果、有意差が認められました。これは、指導試案に基づく授業の、自らの課題をつかみ学習の見通しをもつ活動と自らの課題の解決状況をつかむ活動で、互いの考えを知ったり考えたりしたこと、自らの課題についてまとめる活動の発表で、作った問題の説明と感想を述べ合うことなどの取り組みをとおして育成されたと考えます。
(イ) 既習を活用する力
【表3】は、既習を活用する力の育成状況について、事前・事後テストの結果をまとめたものです。
既習を活用する力は、t検定の結果、有意差が認められました。これは、指導試案に基づく授業の、自らの課題をつかみ学習の見通しをもつ活動でオープンな問題の解決について考えたこと、自らの課題についてまとめる活動で、選んだ問題を自力で作り上げ、解決したこと等の取り組みをとおして育成されたものと考えます。
(ウ) 筋道立てて考える力
【表4】は、筋道立てて考える力の育成状況について、事前・事後テストの結果をまとめたものです。
筋道立てて考える力は、t検定の結果、有意差が認められました。これは、指導試案に基づく授業の、自らの課題の解決状況をつかむ活動と自らの課題についてまとめる活動で学んだことを使って正しく解く取り組みをとおして育成されたものと考えます。
以上のことから、自らの課題を追究する活動を取り入れた創造的に考える力を育てる学習指導試案は、児童の創造的に考える力の育成に妥当であったと考えます。
イ 自らの課題を追究する活動についての意識の状況
指導試案に基づく授業実践後に、研究の手だてである「自らの課題を追究する活動」について児童がどうとらえたかを調べるため意識調査を実施しました。
【表5】は、その調査のなかの、自らの課題を追究する活動に対する感想を観点によって分類し、まとめたものです。
これらの感想から、自らの課題を追究する活動は、児童が好意的に受け入れ、取り組めるものであるととらえることができます。
(2) 中学校第2学年
ア 創造的に考える力の育成状況
指導試案に基づく授業によって、創造的に考える力が育成されたかどうかを調べるために、「多面的にみる力」「既習を活用する力」「筋道立てて考える力」についてテスト問題を作成し、事前と事後に実施しました。
(ア) 多面的にみる力
【表6】は、多面的にみる力の育成状況について、事前・事後テストの結果をまとめたものです。
サイン検定の結果、有意差は認められませんでした。
これは、自らの課題を追究する活動において、設定した課題の内容等が、生徒によっては、解決が容易であったり、あるいは、むずかしすぎたりしたために、多面的に考える力となるまでには至らなかったからと考えます。
また、課題の解決状況の交流が、二人組では比較的なされていましたが、グループではあまり活発ではなかったことで、多面的に考える力となるまでには至らなかったものと考えます。
このことから、課題の設定に際しては、個に応じた適切な支援が必要といえます。また、課題の解決状況の交流に際しては、方法のさらなる検討と時間の確保が必要であるといえます。
(イ)既習を活用する力
【表7】は、既習を活用する力の育成状況について、事前・事後テストの結果をまとめたものです。
t検定の結果、既習を活用する力の変容には、有意差が認められませんでした。
これは、自らの課題を追究する活動において、設定した課題の内容等が、生徒によっては解決が容易であったり、あるいはむずかしすぎたりし、既習の活用とうまく結びつかなかったことによるものと考えられます。
このことから、課題の設定に際しては、適切に支援することが必要と考えます。
筋道立てて考える力は、t検定の結果、有意差が認められました。
これは、自らの課題を追究する活動において、設定した課題を授業で学習した内容と照らし合わせ
ながら、自分のなかで解決していく過程で、筋道立てて考える力が次第に高まってきたものと考えます。
イ 自らの課題を追究する活動についての意識の状況
【表8】は、自らの課題を追究する活動に対する感想を、興味・関心、意欲、有用感・成就感、マイナス傾向の4つの観点でまとめたものです。
【表8】から、記述した22人のうち、18人が好意的な感想を述べていることが分かります。
自分の課題をもつことによって学習が身近なものとなり、課題を解決しながらすすめる学習によって積極的な姿勢で授業に参加し、それが興味・関心や意欲、有用感等につながったものと思われます。
また、マイナス傾向の記述をした生徒が4人いることから、課題設定については机間指導の他にも、個々に対してもっときめ細かに支援すること、学習のまとめ方についてはもっとていねいに説明することなどの工夫が必要と思われます。
おわりに
単元の学習に児童生徒の「自らの課題を追究する活動」を位置付けることによって、創造的に考える力を育てる算数・数学科の学習指導の在り方を明らかにし、学習指導の改善に役立てようと、この研究に取り組んできました。
作成した学習指導試案に基づいた授業実践を小学校5学年と中学校2学年を対象に試みた結果、
自らの課題を追究する活動を取り入れた指導は、小学校では、創造的に考える力を育てることに効果があること、中学校では、創造的に考える力のうち「筋道立てて考える力」を育てることに効果があることがわかりました。
今後は、自らの課題を追究する活動を取り入れた指導を積み重ねながら、創造的に考えることに関する意識の変容もとらえていく必要があると考えます。
最後になりましたが、この研究を進めるにあたり、ご協力いただきました研究協力校の校長先生をはじめとする諸先生方、児童生徒のみなさん、研究協力員の方々に心から厚くお礼申し上げます。
【引用文献・主な参考文献】
1) 植村哲朗 「数学教育における創造性研究の課題」 全国数学教育学会誌 数学教育学研究第5巻 1999
2) 恩田 彰 「創造性教育の展開」 恒星社厚生閣 1994
3) 国立教育研究所 「小・中学生の算数・数学、理科の成績」 東洋館出版社 1998
4) 中島、清水、瀬沼、長崎 「算数の基礎学力をどうとらえるか」 東洋館出版社 1995
5) 横山昌也 「数学教育における創造的思考の評価方法に関する研究」 数学教育学研究紀要
(西日本数学教育学会) 第19号 1993
なお本稿は、平成11、12年度岩手県教育研究発表会発表資料「創造的に考える力を育てる算数・数学科の学習指導に関する研究 −自らの課題を追究する活動をとおして−」を再構成したものです。
授業実践 −−− 小学校 第5学年 「単位量あたりの大きさ」 学習指導案