高等学校「数学基礎」学習指導案
|
学 校 名 |
岩手県立花北商業高等学校 |
| 対象学級 | 第1学年 1学級 |
| (男子24名女子18名計42名) | |
| 指 導 者 | 畠 山 敏 明 |
| 作 成 者 | 畠 山 敏 明 |
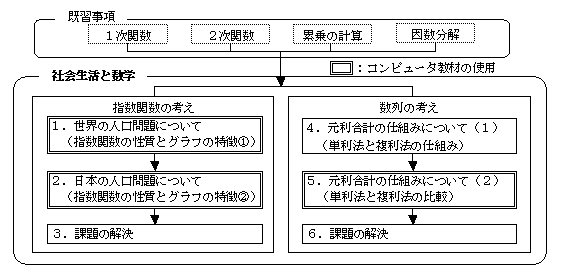
Ⅰ 単元名 「社会生活における数理的な考察 『ア 社会生活と数学』
Ⅱ 単元設定の理由
本単元では、社会生活に現れる事象の変化の様子に新鮮さや驚き、面白さなどを感じさせながら、課題意識をもたせ、解決の過程において指数関数や等比数列などの数学的性質に気付かせたり、その性質や考え方を問題解決に活用させたりすることをひとつの完結性のある学習経験の単位として設定した。
生徒はこれまでに、1次関数や2次関数などの学習において、具体的な事象について数学的に考察し処理する学習を経験している。このような学習は、導入や応用等に限定される場合がほとんどであったが、この科目では、社会生活と数学のかかわりそのものを取り上げるところに、従来の学習との大きな違いがある。
本単元の学習をとおして重点的に指導したいことは、数学の有用性を認識させ、数学への興味・関心を高めることである。指数関数や数列については他の科目の学習内容であるから、理論的な考察には深入りしないことに留意する必要がある。
1 教材観
本単元は、人口の増減や元利合計に現れる指数関数的な数量の変化を視覚的にとらえさせたり、指数関数や等比数列などの数学的性質を見出させたりするとともに、その考え方を課題の解決に活用することにより、数学の有用性を実感させ、数学への興味・関心を高めることがねらいである。
指数関数や等比数列は、社会生活や自然現象のなかにも数多く現れるものであり、変化の様子も単調で、生徒にとっても比較的受け入れやすいもののように思われる。ここでは、指数関数の性質やグラフの特徴、異なる関数や数列の性質の違い、文字の活用などの内容を扱う。ただし、指数関数や等比数列の内容は既習事項ではないので、数学的性質の考察には深入りせず、数量の増減の考察を中心に基本的な内容に留めるものとする。
新学習指導要領では、数学基礎の目標に「社会生活において数学が果たしている役割について理解させ、数学に対する興味・関心を高める」とあり、その内容の「(2)社会生活における数理的な考察 ア社会生活と数学」では、「社会生活を営む上で人間が作った仕組みなどを扱い、それを数理的に考察させる」とある。本単元は、この内容の教材である。
2 生徒観
数学に苦手意識をもつ生徒は少なくないが、生徒の多くは数学の学習を必要なものととらえ、その内容を理解したいと考えている。しかし、小学校中・高学年から中学校、高等学校へと進むにつれて内容が抽象的になり、身近な生活のなかで数学を活用する場面を見出せないことから、生徒の数学に対する興味・関心は次第に薄れる傾向が見られる。
また、身近な生活や、各種情報のなかに現れる数量の変化に、生徒は自然に反応し、数量の増減を直観的に判断するような活動は見られるが、数学の学習と結びつけて思考する場面は少なく、数学の有用性を実感するには至っていない。
3 指導観
本単元では、社会生活に現れる事象の変化の様子に課題意識をもち、その解決の過程において数学の考え方を活用することのよさを認め、数学の有用性を実感し、数学への興味・関心を高めて学習に取り組む生徒の育成をねらいとしている。
そこで、人口増加や元利合計などの社会生活に現れる事象の変化の様子に、新鮮さや驚き、面白さなどを感じさせながら、課題意識をもたせたい。
また、社会生活における事象の変化の様子を、図やグラフを用いて単純化・視覚化し、数学の課題として認識させたい。その解決の過程で、変化の様子を直観的にとらえさせ、結果を予想させたり、数学的な性質に気付かせたりすることにより、数学の見方や考え方のよさや、数学の考え方を活用することのよさを認めさせたい。
さらに、社会生活における事象の変化の様子を、言葉や文字を用いて表し、関数や数列の考えと関連付けさせることによって、社会生活に数学的な考え方が有効に活用されていることを実感させたい。
Ⅲ 単元の指導目標
|
Ⅳ 単元の教材構造

Ⅴ 単元の指導計画(全6時間)
| 第1時 世界の人口問題について <コンピュータ教材>・・・本時 |
| 第2時 日本の人口問題について <コンピュータ教材> |
| 第3時 指数関数の考えを活用した課題の解決 |
| 第4時 元利合計の仕組みについて(1) |
| 第5時 元利合計の仕組みについて(2) <コンピュータ教材> |
| 第6時 等比数列の考えを活用した課題の解決 |
Ⅵ 本時の学習指導
| 1 主題「世界の人口問題について」 | |
| 2 指導目標 | |
| 世界人口の増加の様子から、指数関数の性質やグラフの特徴に気付かせ、さらに1次関数の増加の様子と比較させることにより、人口増加の問題点を明確にし、数理的に考察することのよさを感得させる。 | |
| 3 目標行動 | |
| 指数関数が増加率一定であること、グラフが急激に単調増加することを指摘することができ、世界人口の問題点を、指数関数的な増加と1次関数的な増加を対比して説明できる。 | |
| 4 下位目標行動 | |
| ① 世界人口の増加の状況が、「人口爆発」という課題を抱えていることを確認する。 | |
| ② コンピュータ教材を利用して、資料から年度毎の世界人口の推移をプリントに記入する。 | |
| ③ 30億人、60億人を突破した年や期間から、今後の人口がどのように変化するのか予想する。 | |
| ④ 表よりもグラフの方が、人口の変化の様子をとらえやすいことがいえる。 | |
| ⑤ コンピュータ教材により人口増加の様子をグラフに表すことができる。 | |
| ⑥ 既習の1次関数や2次関数について、グラフの特徴を説明できる。 | |
| ⑦ 1次関数や2次関数とは異なるグラフであることがいえる。 | |
| ⑧ 人口増加の様子から、ある性質をもった新しい関数であると推測することができる。 | |
| ⑨ 1980年から1984年の一年毎の人口増加率を求めることができる。 | |
| ⑩ 一年毎の増加の割合がほぼ一定であることがいえる。 | |
| ⑪ 増加率一定と仮定し、1980年をf(0)、1981年をf(1)、…としたとき、f(0)からf(4)に成り立つ関係を立式できる。 | |
| ⑫ x年後の人口の値を、f(x)=f(0)×(増加率)x の形に表すことができる。 | |
| ⑬ f(10)の値を求め、1990年の人口とほぼ等しいことを確認する。 | |
| ⑭ f(x)=axの形の式が指数関数であることを知る。 | |
| ⑮ 指数関数的に人口が増加した場合の人口が2倍になる年数や、50年後、100年後の人口を予想し、コンピュータを用いて確認する。 | |
| ⑯ 増加率一定と仮定したとき、将来の世界の人口が急激に増加することを指摘できる。 | |
| ⑰ 指数関数について、増加率が一定あること、グラフが急激に単調増加することをいえる。 | |
| ⑱ 「人口爆発」という表現が指数関数的な変化を表していることがいえる。 | |
| ⑲ 20世紀後半から、世界的な規模で人口抑制が課題となってきたことが説明できる。 | |
| ⑳ 穀物生産量の増加の様子を調べ、その様子を1次関数などの言葉を用いて説明できる。 | |
| 21 人口の増加の様子と穀物生産量の増加の様子を比較し、その違いを指摘することができる。 | |
| 22 世界の人口がこのまま増加し続けた場合の問題点を、穀物生産量と関連させ、指数関数的な増加と1次関数的な増加を対比して説明できる。 | |
| G 指数関数が増加率一定であること、グラフが急激に単調増加することを指摘することができ、世界人口の問題点を、指数関数的な増加と1次関数的な増加を対比して説明できる。 | |
5 形成関係図とグルーピング
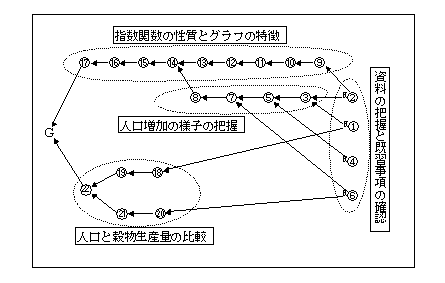
6 本時の展開過程
| 時間 | 主な学習内容 | 展開の流れ | 教材・教具と留意事項 WB:ホワイトボード PC:コンピュータ教材 |
| 5分 | <導入> ・レディネス調査 (①) 人口爆発とは? |
はじめ レディネステスト(教師の補説) |
WB ・世界の人口の増加が人口爆発という問題を抱えていることを確認させる |
|
・プレテスト(G) 人口増加の様子は? 人口増加の規則性は? 人口増加の問題点は? |
プレテスト |
WB・プリント ・人口増加の様子と、人口の増加に派生する諸問題について考えさせ、課題意識を高める ・問題提起にとどめ、深入りしない |
|
|
主題 ・世界の人口問題を考える |
主題の確認(説話) |
WB・プリント ・主題をWBに書き、プリントに記入させる |
|
| 12分 | <展開> 1 人口増加の様子 ・人口資料による把握 (②) |
世界人口の資料収集(作業) | PC・プリント ・提示された資料を利用して、現在の世界人口や、人口の増加の様子を調べさせる |
| ・将来人口の予想 (③) | 今後の人口の予想(問答) |
プリント ・30億人、60億人を突破した年や期間から、今後の人口の変化を予想させる |
|
| ・資料をグラフに表す(④⑤) |
グラフ作成(作業) |
PC・プリント ・グラフによって人口増加の様子を把握しやすくなることに気付かせる ・コンピュータ教材によりグラフを作成し、変化の様子を視覚的にとらえさせる ・データの幅を変えて作成させる |
|
| ・既習のグラフとの比較(⑥⑦) | 既習のグラフとの比較(問答) |
PC ・既習の1次関数や2次関数のグラフと比較させ、異なる性質をもつことを視覚的にとらえさせる |
|
|
〔評価1〕 (⑧) 人口増加の様子から、ある性質をもった新しい関数であると推測できるか? |
新しい関数であるといえるか(教師の補説) | ・グラフの様子や、既習の関数との比較から、新しい性質をもった関数の存在を想起できたか、真偽法で確認する | |
| 18分 | 2 指数関数の式と性質 ・人口増加率はほぼ一定(⑨⑩) |
人口増加率は?(問答) | プリント ・年度毎の増加率がほぼ一定であること計算によって気付かせる ・計算には電卓を用いてもよい |
| ・1980年をf(0)、1981年をf(1)としたときの、f(0)〜f(4)の関係式を立式 (⑪) | 関係式を立式(作業) |
WB・プリント ・社会生活に現れる事象が数学的な処理によって関係付けられることに気付かせる |
|
| ・1980年のx年後の人口f(x) の式を求める (⑫) | x年後の人口を指数関数で表す(説話) |
プリント ・増加率が一定であると仮定する |
|
| ・f(10) の値を求め、1990年の人口とほぼ等しいことを確認 (⑬) | 計算結果が現実の人口とほぼ等しいことを確認(説話) |
WB・プリント ・関数の考えのよさを実感させる |
|
| ・指数関数f(x)=ax(⑭) | 指数関数f(x)=axの定義(説話) |
プリント ・f(x)=axと表せる関数が指数関数であることを説明する |
|
| ・将来の人口の予想と確認(⑮) | 人口の予想と確認(作業) | PC・プリント ・求めた関数により、将来の人口を、コンピュータ教材を用いて求めさせる ・人口の変化の様子を視覚的にとらえさせ、驚きをもたせる |
|
| ・指数関数の増加の特徴(⑯) | 変化の様子の特徴を把握(説話) |
PC ・わずかな増加率でも、急激に変化すること、増加の様子が指数関数のグラフの特徴であることを説明する |
|
|
〔評価2〕(⑰) 指数関数の性質とグラフの特徴がいえるか? |
指数関数の性質とグラフの特徴がいえるか(教師の補説) |
WB・プリント ・指数関数の性質として増加率が一定あること、グラフが急激に単調増加することを認められたか、完成法で評価する |
|
| 10分 | 3 人口増加の問題点 ・人口爆発と人口抑制(⑱⑲) |
人口抑制が必要となってきた理由について(説話) | PC・プリント ・コンピュータ教材により資料を提示する |
| ・食糧生産量の増加の様子(⑳) | 穀物生産量のグラフ(作業) |
PC ・コンピュータ教材により資料を提示する ・食糧生産量は1次関数的に増加していることに気付かせる |
|
| ・人口と食糧生産量の比較(21) | グラフの比較(問答) |
PC・プリント ・指数関数的な増加と1次関数的な増加の様子の違いを確認させる |
|
|
〔評価3〕(22) 世界人口が増加し続けたときの問題点を、増加の様子にふれて説明できるか? |
増加の問題点がいえるか(生徒の発表で補足) | プリント ・食糧生産量と関連させ、指数関数的な増加と1次関数的な増加を対比して説明できるか、生徒に発表させて確認する ・指数関数の考えを用いることによって、人口増加の問題点を明確にできることにふれる |
|
| 5分 | <まとめ> ・ポストテスト(G) |
ポストテスト(教師の補説) | WB・プリント ・完成法で記入させ、生徒に発表させる |
| ・次時の予告 |
時事の学習予告(説話) おわり |
・次時は、日本の人口問題について学習することを知らせる |