第２学年　数学科学習指導案

１　単元名　「図形と方程式」　小単元名−円の方程式−、−直線の方程式−(三省堂「数学�U」)

２　単元について

　本単元は、座標を用いて直線や円など基本的な平面図形の性質や、関係を調べる解析幾何学的な方法を理解させることをねらいとして構成されている。
　これまで生徒は図形について中学校で三角形、四角形、円を中心にその性質を見出したり、把握したりすることを学習し、中学校数学及び「数学�T」においてその計量について学習している。また、直交座標にかかわることについては小学校以来段階的に学習してきているが、それは関数関係の図表示としての扱いであった。
　指導にあたっては、平面における点を座標を用いて表すことにより、図形を数の間の関係として方程式で表すことができることと、逆に方程式で表された数の間の関係を図形で表現することができることを学習させることによって、平面図形とそれを表す方程式の関係をはっきりと認識させたい。

３　単元の目標

関心・意欲・態度
・個々の図形のもつ性質を調べることに興味をもち、図形を表す方程式を積極的に活用しようとする。
数学的な考え方
・図形を表す方程式がどのような考え方で求められるかを説明できる。
・図形を表す方程式の有用性に気付く。
表現・処理
・平面図形を方程式を用いて表すことや、方程式から直線や円を図示することができる。
知識・理解
・平面図形とそれを表す方程式の関係を理解することができる。

４　指導計画(１２時間扱い)

５　本時の学習

(1)　学習項目「円の方程式�@」指導内容『円の方程式の導入』
ア　目標
関心・意欲・態度
・自由な発想で学習に取り組むことができる
数学的な考え方
・円の性質を追求しようとする
表現・処理
・円を言葉で表すことができる
知識・理解
・円は中心からの距離が等しい点の集まりであることを理解することができる
イ　展開

段階	学習内容及び活動	指導上の留意点等
つ か む	１　問題を把握する 【問題】 Ｔ君が点Ｏを中心とする円を右のように描いてみました。Ｔ君の描いた円は円といえるでしょうか、それとも、円とはいえないでしょうか。確かめて下さい。	・学習プリントで提示する ・微妙に歪んだ円を提示することによって生徒の興味を喚起する		グ ル ー プ で の 作 業 ・ 話 し 合 い 活 動
	２　設定の理由を明らかにして課題をつかむ	・「円といえることを確かめる」または「円とはいえないことを確かめる」ことを課題とさせる ・直観や予想を大切にさせる ・まだ、慣れていないので「なんとなく」でもよいものとする
見 通 す	３　解決方法を考える	・習ったことで使えることや、メモをノートに記入させる ・考えだけでなく、道具でもよい ・どんな考えから、どんな解決方法をとるかを言葉で表すことを目標とするが、最初の授業なので図を使ったり、箇条書きでもよいことを指示する
	４　結果を予想する
確かめる	５　自力解決	・見通しにしたがって各自解決をはからせる
	６　集団解決	・グループ毎に考えを発表させ、多様な考え方を練り合わせる
まとめる	７　一般化 ○「円は中心からの距離が等しい点の集まり」	・学習してわかったことを言葉でまとめる
	８　次回予告	・次回は円の方程式について学習することを確認する

(2)　学習項目「円の方程式�B」指導内容『いろいろな条件から自分達で円の方程式を求める』
ア　目標
関心・意欲・態度
・自らすすんで円の方程式を求めるための条件を中心の座標と半径の長さ以外から探そうとする
数学的な考え方
・太郎にかかせるために、いろいろな条件から必要なものを選んで要点を整理して説明することができる。
表現・処理
・自分の考えを文章や式、図を使って表すことができる。
知識・理解 ・円の方程式を求めるための条件の組み合わせが多数存在することを理解できる。
イ　展開

段階		学習内容及び活動	指　導　上　の　留　意　点　等
導入		１　前時の復習をする ○中心の座標、半径から円の方程式を求める	・中心の座標と半径を具体的な数値で与え、求めさせる ・中心の座標と半径が円を決める重要な条件となることを確認する ・学習プリントを配布し、本時の流れを説明する
		２　本時の学習内容を把握する	・答えを出すことよりも、考えを深めることをポイントとする
展 開	つ か む	３　問題を把握する 【問題】 右の円と同じ円を同級生の太郎君にかかせ、さらに円の方程式を求めさせたい。ただし、そのとき、右の円を直接太郎君に見せることはできず、ＡからＦまでの条件をうまく使って指示を出さなくてはならない。条件は少なければ少ないほどよい。太郎君が円の方程式を導けるように「条件を使って円の方程式を求めさせる」を課題として課題の解決計画をたてなさい。	・正確な図が要求されるため、補助線の入った図を用いる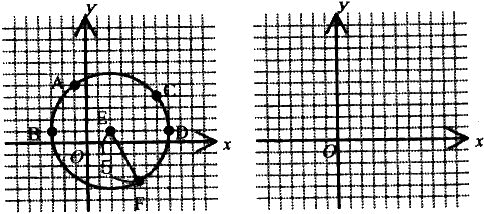		グ ル ー プ で の 作 業 ・ 話 し 合 い 活 動
		４　設定の理由を明らかにして課題をつかむ	・課題は自分の考えた条件（指示）を使って円の方程式を求めることとなる ・図を使ってよいことを確認する ・直観、予想を大切にするが、できれば詳しい説明が入るようにさせる
	見 通 す	５　解決方法を考える	・既習事項と未習事項の相違点や共通点などに注目させる ・習ったことで使えることや、メモをノートに記させる ・どのような考えからどんな解決方法をとるのか考えさせる ・ノートに記入させる ・時間の確保に気を配る
		６　結果を予想する	・円の方程式を予想することを目標とするが、「求めることができる」でもよい
	確 か め る	７　自力解決する	・ノートを見ながら、見通しにしたがって自力解決をはからせる ・途中でもよい
		８　集団解決する	・グループ毎に指名して発表させる ・途中までの場合も考えられるので、その場合は指導者が支援する
	ま と め る	９　解決方法をまとめる 　学習してわかったことを整理し、言葉や式、記号などで表しまとめる ＜予想される生徒の反応＞ ・中心の座標と円周上の１点を条件とするもの ・円周上の３点の座標を条件とするもの	・まとめるものはまとめ、今後の学習に関係あるものは次への課題とする
ま と め		10　学習を振り返って本時のまとめをする
		11　次時の予告 　「３点を通る円の方程式」について学習する	○生徒から出たアイデアを活用する